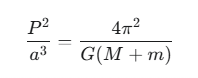ケプラーの法則は、17世紀初頭にドイツの天文学者ヨハネス・ケプラーによって発見された、惑星の運動に関する3つの基本的な法則です。これは、長年にわたるティコ・ブラーエの精密な観測データを分析することで導き出されました。それまで信じられていた「惑星は完全な円軌道を描く」という常識を覆し、近代天文学の扉を開いた画期的な法則です。
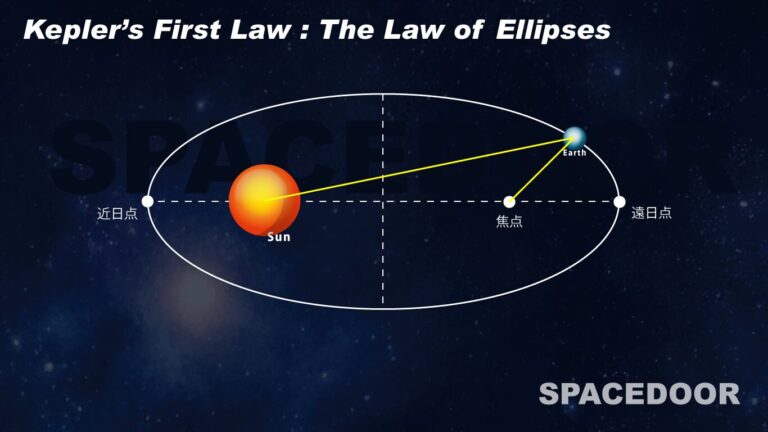
- 第1法則：楕円軌道の法則 (The Law of Ellipses) すべての惑星は、太陽を一つの焦点とする楕円軌道上を運動するという法則です。円は中心が1つですが、楕円には焦点と呼ばれる点が2つあります。惑星が描く軌道では、太陽がその2つのうちの1つに位置しており、もう一方の焦点には何もありません。これにより、惑星と太陽の距離は、公転中に常に変化することになります。軌道上で最も太陽に近づく点を近日点 (Perihelion)、最も遠ざかる点を遠日点 (Aphelion) と呼びます。
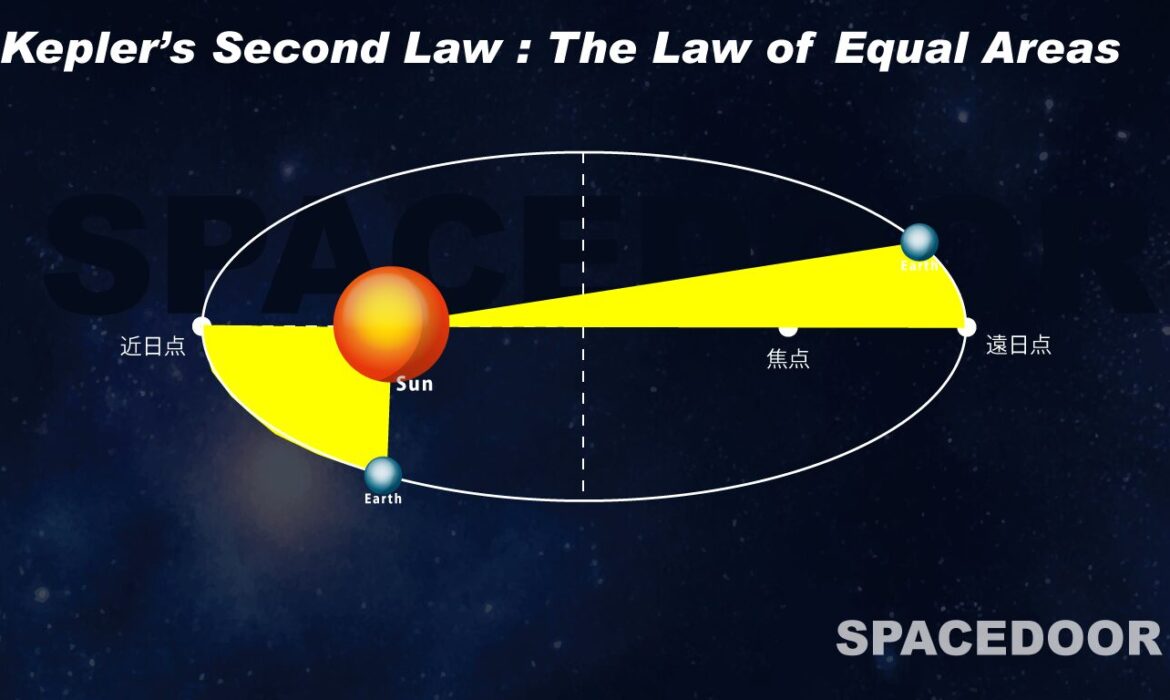
- 第2法則：面積速度一定の法則 (The Law of Equal Areas) 惑星と太陽を結ぶ線分（動径）が、等しい時間内に掃き過ぐる面積は、常に一定であるという法則です。これは、惑星の運動速度が一定ではないことを示しています。具体的には、惑星は太陽に近い近日点付近では速く動き、太陽から遠い遠日点付近では遅く動きます。太陽の引力が強く働く近日点では速度が増し、引力が弱まる遠日点では速度が減少するため、結果として一定時間に描く面積は等しくなります。
- 第3法則：調和の法則 (The Law of Harmonies) 惑星の公転周期（P）の2乗は、その軌道の軌道長半径（a）の3乗に比例するという法則です。数式で表すと P2∝a3 となります。軌道長半径は、楕円の大きさを示す指標で、近日点距離と遠日点距離の平均値に相当します。この法則は、太陽から遠い惑星ほど公転に非常に長い時間がかかることを定量的に示しており、異なる惑星の軌道同士を関係づける重要な法則です。
【もっと詳しく】
ケプラーの法則は、天体の運動を初めて数学的に正確に記述したものであり、アイザック・ニュートンによる万有引力の法則の発見に直接つながりました。ニュートンは、惑星がなぜこのような法則に従って運動するのかを、重力という普遍的な力によって説明しました。
- 第1法則の数学的意味 ケプラーは観測データから惑星の軌道が楕円であることを見出しましたが、なぜそうなるのかは説明できませんでした。後にニュートンは、天体間に働く力が距離の2乗に反比例する「逆2乗の法則」に従う場合、その引力によって束縛された天体の軌道は、円や楕円といった円錐曲線を描くことを数学的に証明しました。惑星の軌道の形は、離心率 (e) という値で表され、e=0 が真円、0<e<1 が楕円となります。
- 第2法則と角運動量保存の法則 面積速度一定の法則は、物理学における「角運動量保存の法則」と本質的に同じです。惑星にかかる太陽の引力は、常に太陽の中心方向に向かって働く「中心力」です。中心力のみが働く場合、その物体の角運動量（回転の勢いを表す量）は常に一定に保たれます。惑星の質量を m、太陽からの距離を r、速度を v とすると、角運動量 L は
（θ は動径と速度ベクトルのなす角）
と表され、これが一定に保たれる結果として、
面積速度
も一定となります。 - 第3法則の一般化 ケプラーが発見した
（kは定数）
という関係は、太陽系の惑星ではほぼ同じ値になります。ニュートンは万有引力の法則からこの定数 k の正体を解き明かしました。
ここで、G は万有引力定数、M は中心天体（太陽）の質量、m は惑星の質量です。太陽の質量 M は惑星の質量 m に比べて圧倒的に大きいため (M≫m)、M+m≈M と近似でき、太陽系のすべての惑星でこの値がほぼ一定になるのです。この一般化された法則により、惑星の公転周期と軌道長半径が分かれば、連星や太陽系外惑星など、様々な天体の質量を推定することが可能になりました。
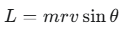（θ は動径と速度ベクトルのなす角）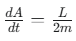
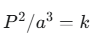（kは定数）
